简介
在计算机科学的广阔领域中动态规划算法犹如一把锋利的钥匙可以开启复杂疑问求解的大门。它不仅广泛应用于计算机科学、运筹学、生物信息学等多个领域还常常被用于解决诸如最短路径、背包难题、字符串匹配等经典疑问。本文将深入剖析动态规划的核心思想与策略框架探讨其本质原理并通过具体实例展示怎样构建和应用动态规划模型。咱们还将讨论动态规划算法的设计步骤、优化技巧及其实际应用场景帮助读者全面掌握这一高效而强大的算法技术。
---
动态规划算法的基本思想是什么?
动态规划算法是一种分阶段求解多阶段决策难题的优化方法。它的基本思想是将一个复杂难题分解为一系列更简单的子疑问并通过保存子疑惑的解来避免重复计算。这类“记忆化”的过程使得算法在面对大规模难题时仍能保持较高的效率。动态规划常常适用于具有更优子结构的疑惑,即难题的更优解可以通过子难题的更优解构造出来。例如,在求解最短路径疑问时,从起点到终点的最短路径能够由从起点到中间点的最短路径和从中点到终点的最短路径组成。动态规划算法通过对这些子难题实施递归求解并保存结果,最终得到全局难题的解。
动态算法的基本思想有哪些?
动态规划的基本思想主要涵盖以下几个方面:
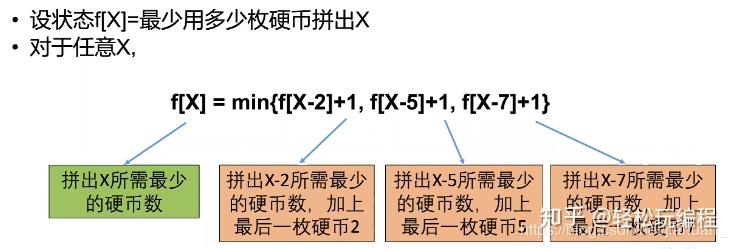
1. 更优子结构性质:任何疑问的更优解都能够通过其子疑惑的更优解构造出来。例如最短路径疑惑中从起点到终点的最短路径能够通过中间点的最短路径组合而成。
2. 重叠子难题性质:在求解期间,许多子难题会被多次求解。通过记忆化存储这些子疑惑的解能够避免重复计算,增强算法效率。
3. 状态转移方程:动态规划的核心在于建立状态转移方程,描述从一个状态转移到另一个状态的过程。状态转移方程一般是通过分析疑问的更优子结构得出的,用以表示疑惑的状态变化规律。
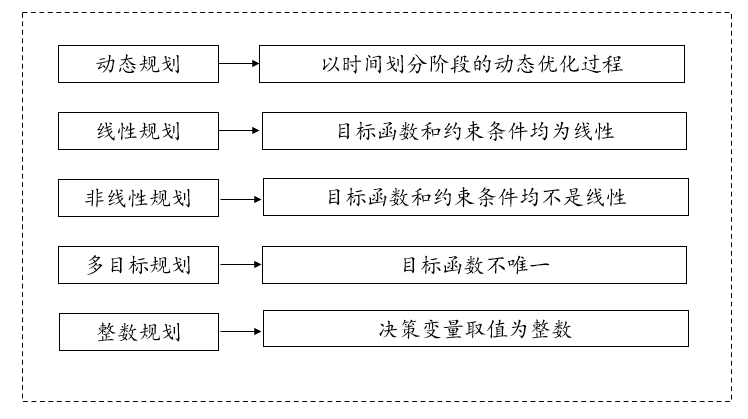
4. 递归与迭代:动态规划可通过递归形式实现,但为了避免重复计算,往往利用自底向上的迭代方法。迭代方法从基础状态开始逐步推导出最终解,此类方法也称为动态规划表法。
动态算法的基本思想涵盖
动态规划算法的基本思想包含以下几方面:
1. 状态定义:首先需要明确疑问的状态,定义状态变量和状态空间。状态变量多数情况下表示当前难题的一个关键特征,状态空间则包含了所有可能的状态组合。
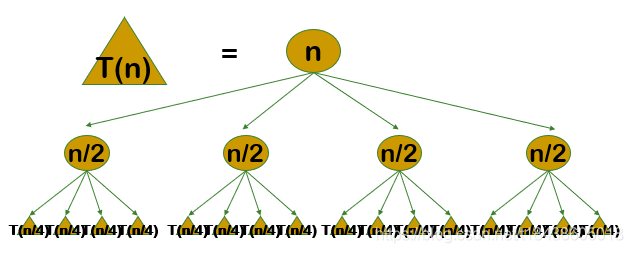
2. 状态转移方程:基于状态定义,建立状态转移方程,描述从一个状态转移到另一个状态的过程。状态转移方程反映了不同状态之间的关系,以及怎么样通过子难题的解来构造当前状态的解。
3. 边界条件:定义疑问的初始状态或边界条件,这是动态规划算法的基础。边界条件多数情况下是难题的最基本情形,可直接求解。
4. 记忆化搜索:为了增进算法效率,采用记忆化搜索的方法,将已求解的子疑惑的解存储起来,避免重复计算。这一步骤是动态规划算法的核心之一,保障了算法的时间复杂度得以优化。
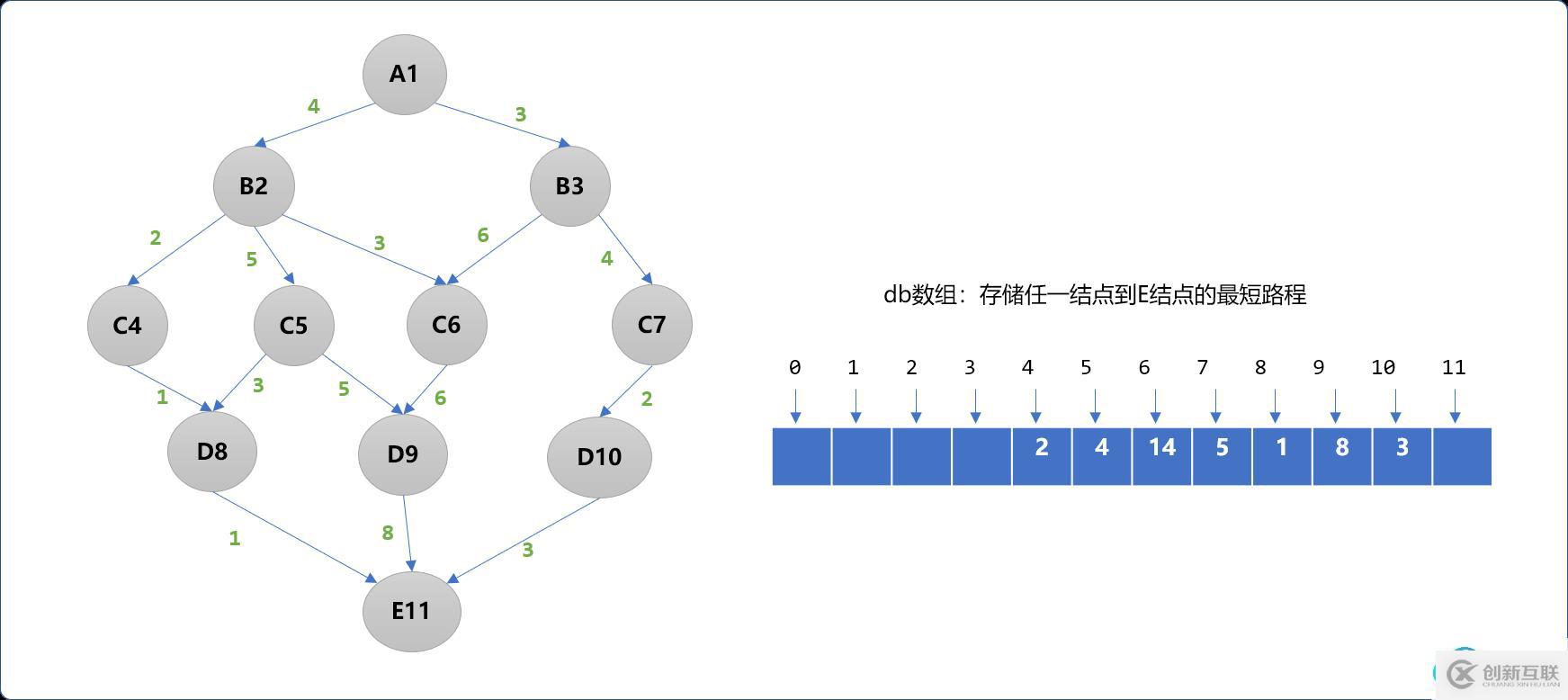
5. 递归与迭代:动态规划算法能够通过递归办法实现,但为了避免重复计算,一般利用自底向上的迭代方法。迭代方法从基础状态开始逐步推导出最终解这类方法也称为动态规划表法。通过递推的办法,能够有效地构建难题的解。
动态算法
动态规划算法是一种要紧的算法设计技术,广泛应用于解决各种优化难题。其核心思想在于将复杂疑惑分解为更简单的子疑问,并通过记忆化存储子疑惑的解来避免重复计算。动态规划算法特别适用于具有更优子结构和重叠子难题性质的疑问,如最短路径、背包难题、字符串匹配等。通过理解动态规划算法的基本思想,咱们可更好地掌握其设计方法和应用场景,从而在实际疑问中灵活运用这一强大工具。
动态计算法
动态计算法是动态规划算法的一种扩展形式,它强调对疑问实施动态的、逐步的计算。在动态计算法中,疑问被划分为多个阶段,每个阶段包含一系列状态和决策。通过递归地求解每个阶段的更优解,并将这些局部更优解组合成全局更优解。动态计算法的核心在于利用状态转移方程,描述从一个阶段到下一个阶段的状态变化过程。通过此类方法,能够有效地应对复杂疑惑,并且在求解期间避免不必要的重复计算。