矩阵排列：详解在矩阵排列中的应用与技巧

一、引言

矩阵排列是计算机科学、数据科学和人工智能领域中的一个要紧概念。随着人工智能技术的不断发展在矩阵排列中的应用越来越广泛为众多行业带来了革命性的变革。本文将详细介绍在矩阵排列中的应用与技巧帮助读者更好地理解和掌握这一技术。

二、矩阵排列概述

1. 矩阵排列的概念

矩阵排列是指将一组数据依照一定的规律实行排列形成一个矩阵。矩阵排列在数学、物理、计算机科学等领域中有着广泛的应用。例如在图像解决中将图像像素值排列成矩阵便于实行后续应对；在机器学中将特征数据排列成矩阵便于构建模型。

2. 矩阵排列的意义

矩阵排列是指利用人工智能技术，对矩阵实排列和优化。矩阵排列的意义主要体现在以下几个方面：

（1）提升数据解决效率：通过矩阵排列，可简化数据应对过程，增强计算速度。

（2）优化算法性能：合理的矩阵排列有助于增进算法的收敛速度和准确性。

（3）减少存空间：矩阵排列可减少数据的冗余，减低存空间需求。

（4）便于模型构建：矩阵排列为机器学模型的构建提供了基础。

三、矩阵排列的应用与技巧

1. 应用领域

（1）图像应对：在图像应对中，将图像像素值排列成矩阵，便于实边缘检测、滤波、图像增强等操作。

（2）语音识别：在语音识别中，将语音信号排列成矩阵，便于提取特征构建识别模型。

（3）自然语言应对：在自然语言应对中，将文本数据排列成矩阵便于实行词性标注、命名实体识别等任务。

（4）推荐系统：在推荐系统中，将使用者表现数据排列成矩阵，便于构建协同过滤模型，实现个性化推荐。

2. 技巧与方法

（1）数据预应对：在实行矩阵排列之前，需要对数据实行预解决，涵去噪、归一化、降维等。

（2）矩阵分解：通过矩阵分解技术，将原始矩阵分解为多个子矩阵，便于后续应对。

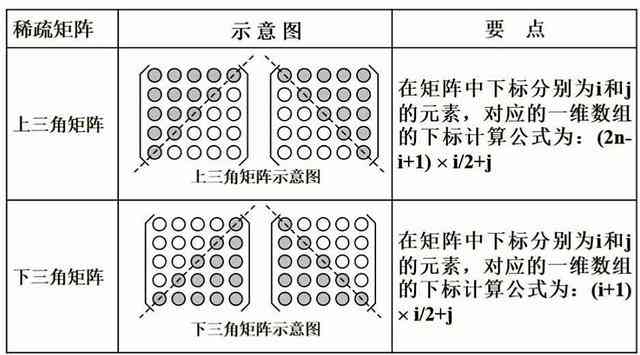
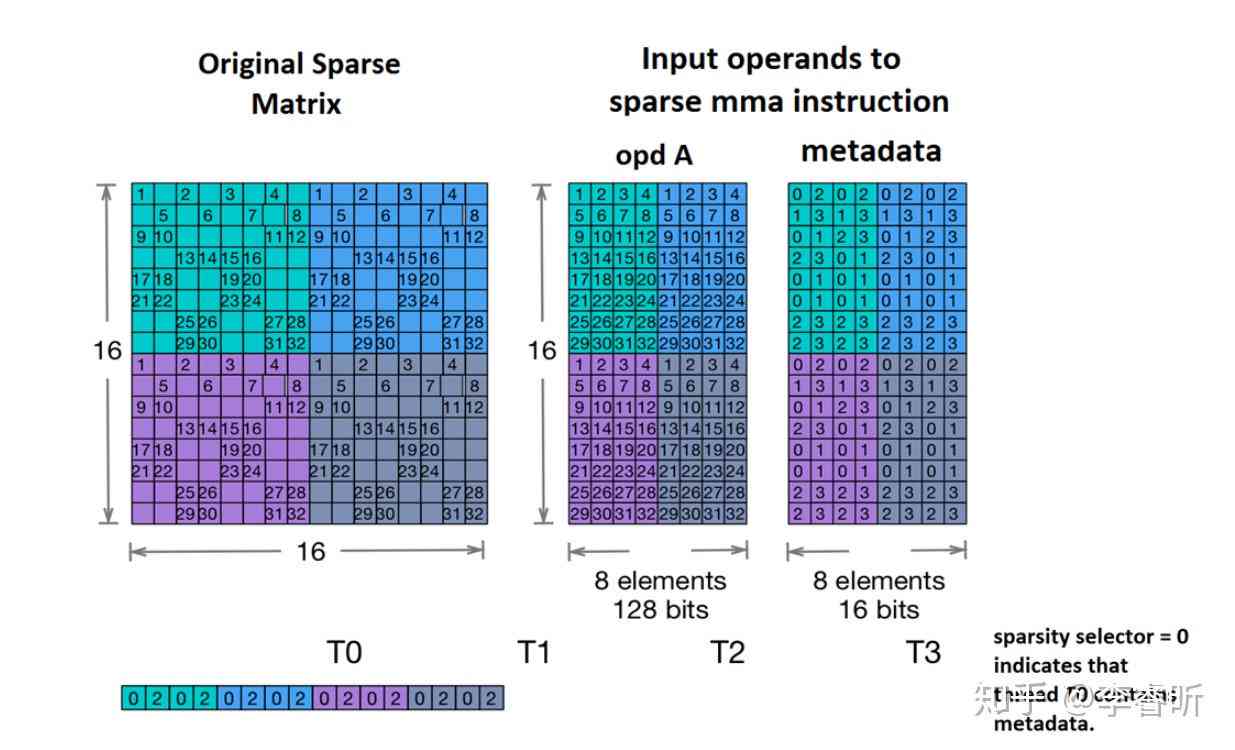
（3）稀疏矩阵：对大型矩阵，可以采用稀疏矩阵存形式，减少存空间和计算复杂度。

（4）特征选择：在矩阵排列期间，合理选择特征，可升级模型的性能。

（5）优化算法：采用高效的优化算法，如梯度下降、牛顿法等，增强矩阵排列的效率。

四、案例分析

以图像应对为例，介绍矩阵排列在实际应用中的具体操作。

1. 数据预解决：对图像实行去噪、归一化等操作，升级图像品质。

2. 矩阵排列：将图像像素值排列成矩阵，便于后续应对。

3. 矩阵分解：采用矩阵分解技术，将原始图像矩阵分解为多个子矩阵。

4. 特征提取：从子矩阵中提取特征，如边缘、纹理等。

5. 模型构建：利用提取的特征，构建图像分类或识别模型。

6. 模型训练与优化：通过训练数据集对模型实行训练，采用优化算法提升模型性能。

五、总结

矩阵排列技术在计算机科学、数据科学和人工智能领域具有必不可少的应用价值。通过本文的介绍，咱们熟悉了矩阵排列的基本概念、应用领域以及技巧与方法。在实际应用中，合理运用矩阵排列技术，可优化算法性能，提升数据解决效率，为各个行业带来创新性的变革。随着人工智能技术的不断进步，矩阵排列的应用将越来越广泛，为人类社会的发展贡献更多力量。