向量集成为子空间的充要条件及其判定方法详解

一、引言

向量空间是线性代数中的基本概念，而子空间则是向量空间的一个关键性质。本文将详细介绍向量集成为子空间的充要条件及其判定方法帮助读者更好地理解子空间的概念及其在实际应用中的意义。

二、子空间的定义与性质

1. 子空间的定义

子空间是指一个向量空间的非空子 ，假如其本身对加法和标量乘法操作也构成一个向量空间，则称为原向量空间的子空间。

2. 子空间的性质

（1）子空间必须包含零向量（原点），一维、二维、三维向量空间以及n维向量空间均应包含零向量。

（2）子空间中的任意两个向量之和仍然属于该子空间。

（3）子空间中的任意向量与标量相乘的结果仍然属于该子空间。

三、向量集成为子空间的充要条件

依据子空间的定义与性质，咱们可得出向量集成为子空间的充要条件：

1. 子空间必须包含零向量。

2. 子空间对加法和标量乘法操作封闭。

下面咱们分别证明这两个条件的必要性及充分性。

1. 必要性

（1）若一个非空子集不包含零向量，则它不可能是子空间。

（2）若一个非空子集对加法或标量乘法不封闭，则它也不可能是子空间。

2. 充分性

设U是向量空间V的一个非空子集，若U满足以下条件：

（1）零向量属于U。

（2）对于任意u1, u2属于U，u1 u2仍然属于U。

（3）对于任意u属于U和任意标量a，au仍然属于U。

则U是V的一个子空间。

四、子空间的判定方法

1. 线性无关性判断法

对于一个向量 ，若是其中任意n个向量都线性无关那么这个向量 就是一个子空间。

2. 子集的交集法

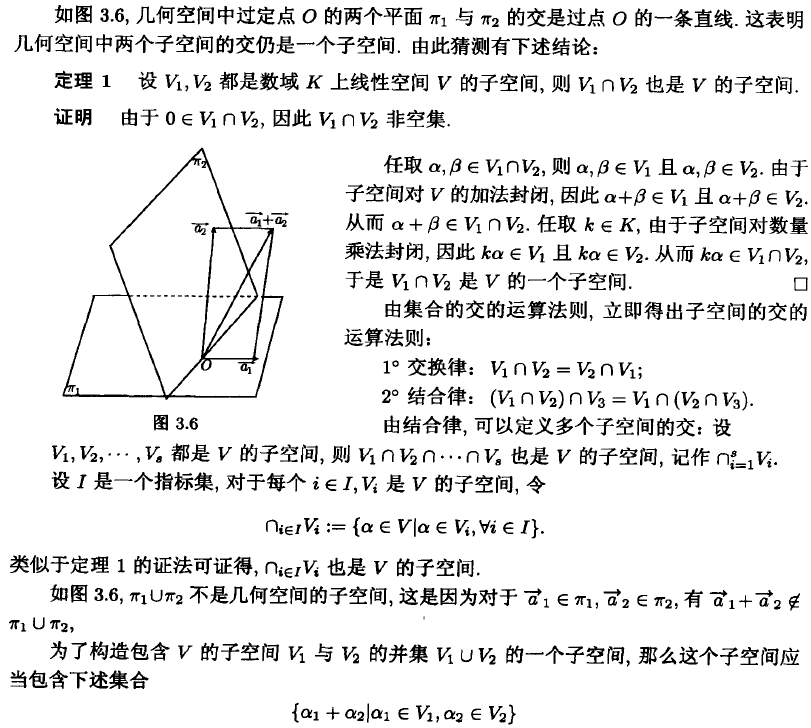
设V是域K上的向量空间，V1和V2是V的两个子空间。若V1∩V2非空，则V1∩V2也是V的一个子空间。

3. 子集的并集法

设V是域K上的向量空间V1和V2是V的两个子空间。若V1∪V2非空，且V1∪V2对于加法和标量乘法封闭，则V1∪V2是V的一个子空间。

五、实例分析

例子1：设域K是实数的 R，并设向量空间V是几里得空间R3。取W为最后的分量是0的V中所有向量的 。易验证W是V的一个子空间，因为它满足子空间的定义与性质。

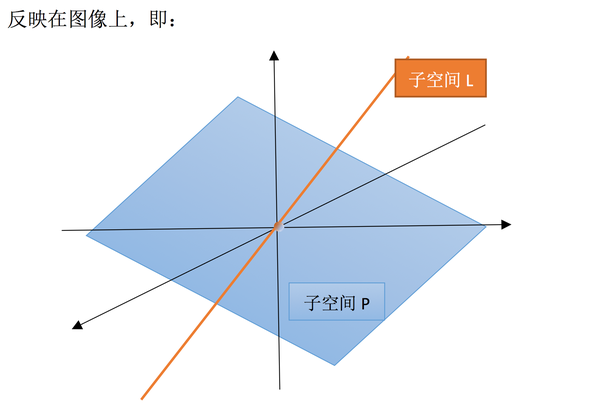
例子2：设V是实数域上的二维向量空间，V1是x轴上的点构成的子集，V2是y轴上的点构成的子集。易验证V1和V2都是V的子空间，且V1∩V2是V的一个子空间。

六、总结

本文详细介绍了向量集成为子空间的充要条件及其判定方法通过定义与性质的阐述使得读者可以更好地理解子空间的概念。在实际应用中，掌握子空间的判定方法有助于咱们分析向量空间的性质从而应对实际疑惑。