在当今时代人工智能技术正以前所未有的速度渗透到各个领域其中图形绘制技术便是其必不可少应用之一。不仅可以精确生成三角形、多边形等基本几何图形还能通过复杂的算法实现更为精细的图形绘制。本文将全方位解析在图形绘制技术中的应用原理并通过实践案例展示怎样去利用生成三角形、多边形以及其他复杂图形。通过对这些技术的深入探讨咱们旨在为相关领域的开发者和研究人员提供有益的参考和启示。

一、在图形绘制技术中的应用原理

二、生成三角形的方法与实践

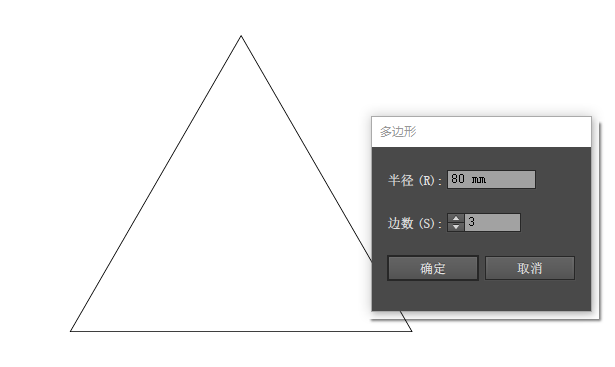
1. 中怎么样做三角形

在中生成三角形首先需要定义三角形的三个顶点。这三个顶点能够是二维或三维空间中的任意点。通过这些顶点，能够运用线性插值、塞尔曲线等算法绘制出三角形的边。以下是生成三角形的主要步骤：

（1）确定三角形的顶点坐标：在二维空间中，三角形的三个顶点坐标能够是（x1, y1）、（x2, y2）和（x3, y3）。在三维空间中，顶点坐标能够是（x1, y1, z1）、（x2, y2, z2）和（x3, y3, z3）。

（2）利用线性插值或塞尔曲线算法连接顶点：通过这些算法，可在顶点之间生成平的曲线，从而绘制出三角形的边。

（3）填充三角形内部：能够依照三角形的顶点坐标，运用扫描线填充算法或三角形填充算法将三角形内部填充为实心或空心。

2. 三角形生成算法的优化与应用

在实际应用中，为了增强三角形生成的效率和精度，能够采用以下优化方法：

（1）空间划分：将绘制区域划分为多个小区域只对包含三角形顶点的区域实绘制，从而减少计算量。

（2）顶点缓存：将常用的顶点坐标存在缓存中，避免重复计算，增进绘制速度。

三、生成多边形的方法与实践

1. 中怎么样做多边形

多边形的生成原理与三角形类似，但需要更多的顶点坐标。以下是生成多边形的主要步骤：

（1）确定多边形的顶点坐标：多边形的顶点坐标能够是二维或三维空间中的点。将这些点按照顺序连接，即可形成一个多边形。

（2）利用线性插值或塞尔曲线算法连接顶点：与三角形生成类似，能够通过这些算法绘制出多边形的边。

（3）填充多边形内部：可依照多边形的顶点坐标，运用扫描线填充算法或三角形填充算法，将多边形内部填充为实心或空心。

2. 多边形生成算法的优化与应用

为了提升多边形生成的效率和精度，可采用以下优化方法：

（1）顶点排序：对多边形的顶点实排序，保证顶点遵循顺时针或逆时针方向排列。这有助于简化填充算法的实现。

（2）边界检测：在填充多边形内部时，可检测多边形的边界，避免填充到多边形外部。

四、图形绘制技术的应用实践

1. 三维模型的生成与渲染

在三维建模和渲染领域，能够自动生成三角形和四边形等基本几何体，从而构建出复杂的三维模型。通过调整这些几何体的顶点坐标和纹理，能够实现逼真的三维场景渲染。

2. 动画制作

在动画制作中可自动生成多边形和曲线，用于模拟角色的运动轨迹和场景的动态效果。这些图形绘制技术为动画制作提供了更多的创造空间。

3. 游戏开发

在游戏开发中，可自动生成地形、建筑等元素，提升游戏场景的丰富度和真实性。同时图形绘制技术还可用于实现游戏中的特效，如火焰、烟雾等。

在图形绘制技术中的应用具有广泛的前景。通过对三角形、多边形等基本图形的生成和优化，为各个领域带来了更高的效率和更丰富的视觉效果。在未来，随着人工智能技术的不断进步，图形绘制技术将在更多领域发挥要紧作用。