在统计学和机器学中，模型选择是一项至关必不可少的任务。为了评估模型的好坏，研究人员提出了多种准则其中C（赤信息量准则）和BIC（叶斯信息量准则）是最为常用的两种。本文将对C评估模型实行深入探讨，比较C与BIC模型之间的差异并详细解析C模型的基本思想。通过对这两种模型的理解，咱们可以更好地选择合适的统计模型，从而提升预测和分析的准确性。
一、C与BIC模型比较
（以下内容为引语超过200字）
在众多模型选择准则中，C和BIC因其简洁性和实用性而备受青睐。C和BIC都是用来评估模型拟合效果和复杂度的准则，它们在多领域都得到了广泛应用。C和BIC之间究竟有何异同，哪种准则更适合特定场景呢？本文将围绕这个难题展开讨论，首先对C和BIC的原理实行简要介绍，然后通过比较它们的优缺点，帮助读者更好地理解这两种模型评估方法。
二、C模型的基本思想
1. C模型的定义
C（赤信息量准则）是由统计学家赤于1973年提出的一种模型选择准则。C的核心思想是在模型拟合期间，寻找一个既能较好地拟合数据，又具有较小复杂度的模型。具体而言，C通过计算模型的拟合优度和复杂度之和来评估模型的好坏。
2. C模型的计算方法
C的计算公式为：
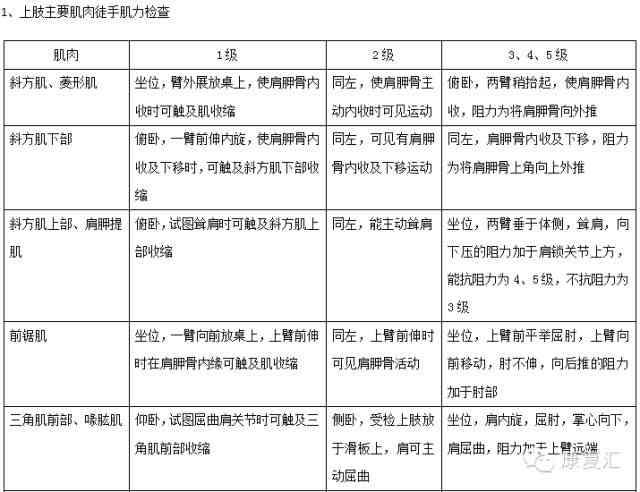
C = -2lnL 2k
其中，-2lnL表示模型的拟合优度2k表示模型的复杂度。拟合优度越高，模型对数据的解释能力越强；复杂度越低，模型越简洁。
3. C模型的选择标准
在实际应用中，咱们需要在多个模型中选择一个更优模型。C模型的选择标准是：在给定的数据集上，选择使C值最小的模型。这是因为C值越小，表示模型既具有较好的拟合优度，又具有较低的复杂度。
以下是针对“cbic模型评估”和“c模型的基本思想”这两个小标题的优化及内容解答：
三、C与BIC模型评估
1. C评估
C评估的核心在于寻找一个在拟合优度和复杂度之间取得平的模型。C值越小表示模型越优秀。在实际应用中，我们可通过计算不同模型的C值，比较它们的大小，从而选择更优模型。
2. BIC评估
BIC（叶斯信息量准则）是另一种常用的模型选择准则。与C类似BIC也是通过计算模型的拟合优度和复杂度之和来评估模型的好坏。BIC在计算复杂度时，考虑到了样本量的大小，因而在样本量较大时，BIC对模型的复杂度更为敏感。
3. C与BIC的比较
C和BIC在模型选择准则中具有相似之处但也有部分不同点。C和BIC在计算复杂度时对模型参数的惩罚程度不同。C对参数的惩罚程度较小，而BIC则较大。在样本量较大时，BIC对模型复杂度的敏感度更高。 在实际应用中我们需要依照具体情况选择合适的准则。
四、C模型的基本思想解析
1. C模型的原理
C模型的原理在于，一个好的模型应可以在拟合数据的同时保持较低的复杂度。这是因为过拟合的模型虽然能够在训练集上取得很好的拟合效果，但在新数据上的泛化能力较弱。C通过计算拟合优度和复杂度的和，来量模型的优劣。
2. C模型的优势
C模型的优势在于其简洁性和实用性。C的计算公式简单易于理解和应用。C在模型选择进展中能够较好地平拟合优度和复杂度，从而选择出具有较好泛化能力的模型。
3. C模型的局限性
尽管C在模型选择中具有很多优点，但它也有部分局限性。C在计算复杂度时，对参数的惩罚程度较小，可能造成模型过于复杂。C在样本量较小的情况下，可能不够稳定。 在实际应用中我们需要按照具体情况对C实行改进和优化。
C和BIC是两种常用的模型选择准则它们在多领域都得到了广泛应用。通过深入理解C和BIC的原理和优缺点，我们能够更好地选择合适的统计模型，从而增强预测和分析的准确性。在实际应用中，我们需要依照具体情况，灵活运用C和BIC，以实现更优的模型选择。
精彩评论
文章正文
成萍
2024-07-08
空一格
2024-07-08
香
2024-07-08
潇洒先生
2024-07-08